C. Menor-Salván, v1 Nov. 2022.
El método de Lowry resulta de la fusión de dos ensayos
La determinación de proteínas por el método Lowry se basa en la unión de dos ensayos que se conocían previamente: el ensayo del biuret para proteínas y la reacción de Folin-Ciocalteau. La combinaicón de los dos métodos mejora mucho la sensibilidad de la reacción. Esta es, además, un buen modelo para entender como funciona la colorimetría, o espectrofotometría en el visible.
- Ensayo de biuret
En la primera parte del ensayo (seguir el guión!), utilizamos un reactivo preparado en el momento (reactivo C), formado por una mezcla de una solución de sulfato de cobre (reactivo B1), una solución de de tartrato sódico-potásico (reactivo B2) y una solución alcalina conteniendo NaOH y Na2CO3 (reactivo A). La mezcla se prepara en el momento, pues la sal de cobre en medio alcalino tiende a precipitar. El tartrato actúa como estabilizante, formando un complejo de cobre. Cuando el reactivo de biuret recién preparado se mezcla con la solución de proteínas a ensayar, se produce la formación de un complejo de la proteína con cobre, acompañado de la desnaturalización de la proteína.
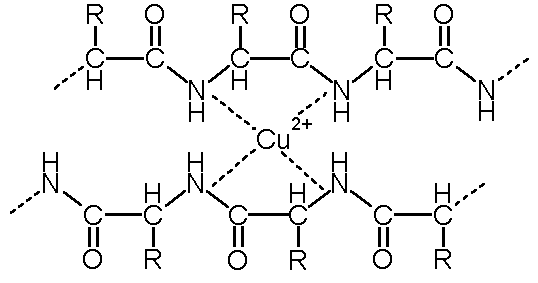
La reacción se denomina de biuret, debido a que se basa en la formación del complejo de cobre con el dímero de urea, biuret, con el que forma un complejo fuertemente coloreado:
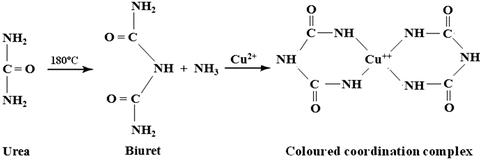
El cobre forma un complejo tetracoordinado con los iminos del enlace amida o peptídico. La distancia entre los grupos imino en el péptido es perfecta para la formación del complejo. Es necesario que el reactivo sea alcalino, para desprotonar las proteínas y estabilizar el complejo de cobre.
- Reaccion de Folin
Una vez formado el complejo de cobre con la proteína, las tirosinas (aminoácido con un radical fenólico) presentes en ella quedan accesibles para que tenga lugar la reacción de Folin-Ciocalteu, que se basa en la oxidación de los fenoles mediante el reactivo de Folin. Este reactivo es, usualmente, una mezcla de ácido fosfomolíbdico y ácido fosfowolfrámico, o bien ácido fosfomolíbdico solo. El molibdeno y el wolframio tienen gran similitud en sus propiedades químicas. La reacción se basa en la reducción parcial del compuesto de partida, con Mo(VI) y/o W(VI), a una estructura compleja con el molibdeno y wolframio parcialmente pentavalentes, llamada ión de Keggin, de color intensamente azul. La estructura de los iones de Keggin es [PW12O40]3- o [PMo12O40]3-
La reducción en el caso del molibdeno no da una única especie, sino una mezcla de especies que denominamos azul de molibdeno. La reacción típica es:
H3PMo12O40 + fenol = [H4PMo(VI)8Mo(V)4O40]3-
El fenol que va a producir el azul de molibdeno es el grupo R de los resíduos de tirosina en la proteína.
La producción de color azul es proporcional a la concentración de proteínas presentes, por lo que es una reacción muy indicada para la determinación colorimétrica.
Calculando la concentración de proteína
Una vez terminada la reacción, determinamos la intensidad del color producido en forma de absorbancia, es decir, una medida del ratio entre la luz incidente en la muestra y la luz transmitida por la muestra, a una longitud de onda complementaria. Específicamente, la absorbancia es:
A=ln I0/I
Donde I0 es la intensidad de luz incidente sobre la muestra, e I es la intensidad transmitida. Esta es la razón por la que la absorbancia no tiene unidades.
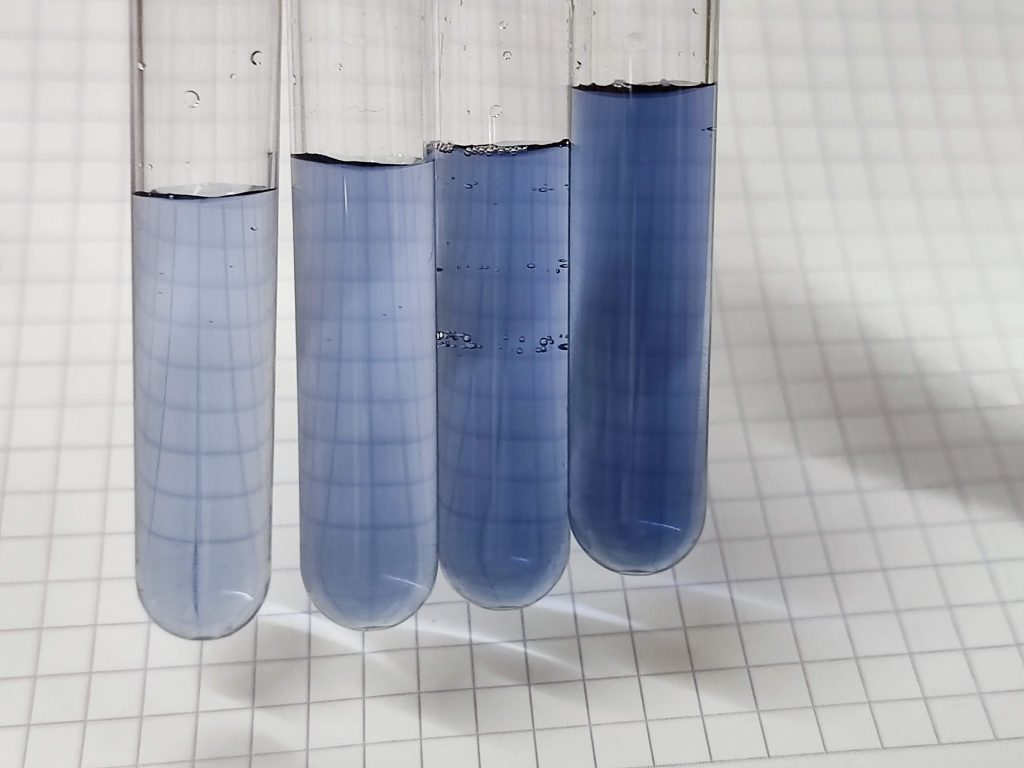
En nuestro caso se mide la absorbancia a 580 nm (luz amarillo anaranjada). Vemos el azul de molibdeno de este color azul intenso, debido a que absorbe la luz incidente en toda la banda entre el amarillo y el rojo. En términos técnicos, el azul de molibdeno es nuestro cromóforo, es decir, la molécula responsable del color. Los datos reales obtenidos en uno de los experimentos son estos:

Los tubos 0 a 4 son la recta patrón, que usaremos como referencia para calcular la concentración en los tubos 5 y 6, que son la muestra problema. La ley de Lambert-Beer establece que la absorbancia es directamente proporcional a la concentración del analito y la longitud del haz de luz que atraviesa la muestra:
A = E x C xL
donde E hace referencia a una constante, característica de cada molécula o cromóforo, llamada coeficiente de extinción molar o también coeficiente de atenuación molar. L, la longitud del haz de luz, la controlamos con las cubetas de espectrofotometría, que siempre tienen 1 cm de anchura interna, de modo que podamos eliminar este término.
Dado que esta ecuación es una recta, podríamos ajustar los datos de absorbancia medidos en los tubos 1 a 4 (considerando que el tubo cero, llamado blanco, tiene absorbancia cero. En todos los ensayos de este tipo siempre debe haber una muestra en blanco) mediante regresión lineal, bien utilizando el clásico y obsoleto método manual con papel milimetrado, o bien un software adecuado. Con los datos obtenidos, tenemos este ajuste:
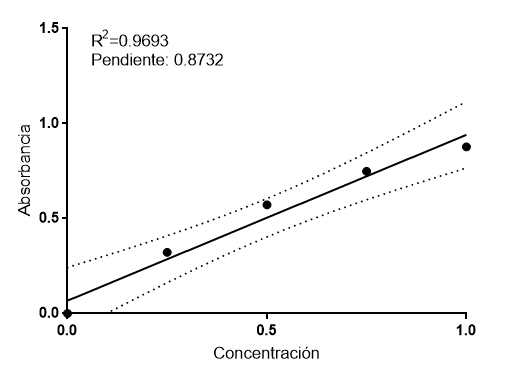
Aunque la linealidad es buena, no todos los puntos están sobre la recta. De hecho, más bien los puntos configuran una curva. Por ello, el rango de error (líneas punteadas) es bastante elevado. Después volveremos a ello. Fijémonos en la pendiente: es el coeficiente de atenuación molar, que nos arroja un valor de 0.8732 ml/mg (obsérvese que el coeficiente de atenuación molar tiene unidades de inversa de concentración). Usando interpolación en esta recta, obtenemos que las concentraciones para los tubos 5 y 6 son:
C5= 0.368 mg/ml
C6= 0.565 mg/ml
Ahora, deshaciendo la dilución, teniendo en cuenta el volumen en los tubos sin reactivos, es decir, un volumen total de 400 ul (agua + patrón o muestra): 0.368 mg/ml * 400 ul = 120 ul * Cproblema
Entonces, Cproblema = 1.23 mg/ml
Usando el tubo 6 (siguiendo la referencia de la tabla anterior), tendríamos 0.565 mg/ml * 400 ul= 200*Cproblema
Entonces, Cproblema = 1.13 mg/ml
Volvamos al problema de la linealidad: Realmente la ley de Lambert-Beer es una aproximación, válida sólo a concentraciones bajas. A concentraciones altas el color es muy intenso y la ley de Lambert-Beer se desvía de la linealidad. Si aplicamos la ecuación de la ley lineal de Lambert-Beer a los datos de cada tubo de la tabla anterior, obtenemos las atenuaciones molares, E, en cada tubo:
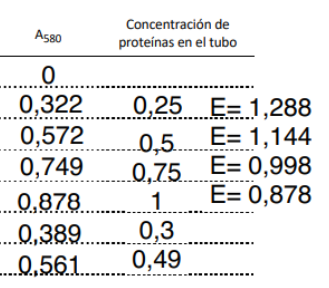
¿que observamos? que el valor del coeficiente de exinción molar en cada tubo va disminuyendo. Es decir, la pendiente va cayendo. O sea, que al aumentar la intensidad del color, vamos perdiendo sensibilidad. Vamos a calcular las concentraciones usando los valores próximos. Por ejemplo, para el tubo 5 (A=0.389) vamos a usar el tubo 1 (A=0.322) como referencia, por tanto, aplicando la ley lineal de Lambert-Beer:
0.389 = 1.288 * C5 , por lo que C5=0.30 mg/ml. Deshaciendo la dilución como anteriormente, tenemos que:
0.30 mg/ml * 400 ul = 120 ul * Cproblema
Entonces, Cproblema = 1.00 mg/ml
Para el tubo 6 (A=0.561) usaremos como referencia el tubo 2, cuya absorbancia es muy próxima. Por tanto:
0.561 = 1.144 * C6 , por lo que C6=0.49 mg/ml. Deshaciendo la dilución como anteriormente, tenemos que:
0.49 mg/ml * 400 ul = 200 ul * Cproblema
Entonces, Cproblema = 0.98 mg/ml
Ahora es cuando podemos revelar que la concentración real que hemos usado para el problema de este experimento es 1.00 mg/ml. Se puede observar entonces la importancia de las desviaciones de la linealidad y cómo, en efecto, en la zona de menor concentración podemos tener datos más precisos. Por ello, al realizar una determinación colorimétrica, como las determinaciones de concentración de proteínas, es conveniente utilizar soluciones lo más diluidas posible, de modo que la instrumentación pueda detectar las variaciones de color, pero sin que los efectos no lineales afecten a la determinación.
Ajuste a hipérbola rectangular
Ahora hagamos un ajuste de los datos un poco más complejo, realizando una regresión no lineal a una función hiperbólica:
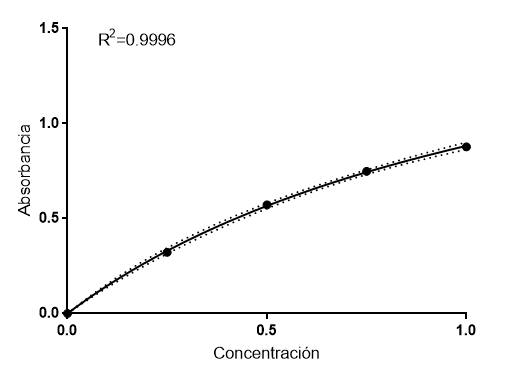
Como se puede ver, el ajuste es casi perfecto y por tanto, comprobamos que la Ley de Lambert-Beer es, realmente, únicamente válida para soluciones diluidas. La razón de ello es que una solución diluida es homogénea e isótropa, y la atenuación de la luz responde a una ecuación clásica de atenuación de radiación:
I=I0e-EL
de la cual se deduce la ecuación lineal de Lambert-Beer, al considerar la definición de absorbancia que dimos anteriormente.
Incluyendo todo el rango de concentración, podríamos definir, de manera empírica, esta función hiperbólica:
A= Amax*C/(C50 + C)
Donde Amax es la máxima absorbancia que podemos obtener, en este caso sería 2. C50 sería la concentración de proteína que necesitamos para tener el 50% de la absorbancia máxima, en este caso 1.26 mg/ml. Usando este ajuste, tenemos que C5=0.30 mg/ml y que C6=0.49 mg/ml, por lo que, de nuevo, obtenemos unos valores perfectamente coincidentes con el valor real. Curiosamente, esta ecuación que hemos usado es exactamente la misma que la ecuación de Michaelis-Menten.
Ajuste a un polinomio de segundo grado
El ajuste hiperbólico anterior, de nuevo, es una aproximación, pero no describe realmente lo que está ocurriendo. Rigurosamente, la generalización de la ley de Lambert-Beer es un polinomio de segundo grado. Si realizamos el ajuste polinomial, obtenemos este resultado:
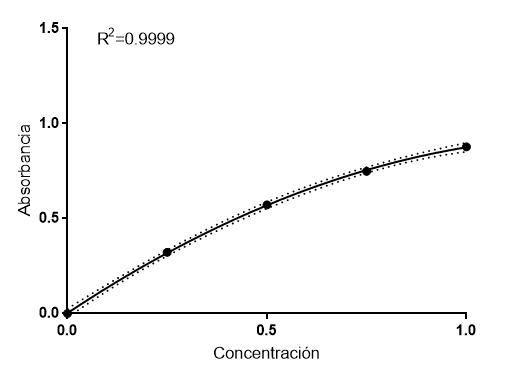
Como puede verse, el ajuste es perfecto y las líneas de error prácticamente han desaparecido. Ya hemos encontrado lo que ocurre realmente a concentraciones altas. La ley de absorbancia o ley de Lambert-Beer generalizada es:
A= E*C – S*C2
Donde E define el coeficiente de atenuación molar lineal y S define el coeficiente de atenuación molar no lineal. El segundo término de la ecuación recoge los efectos no lineales que se producen a alta concentración. Esta ecuación es más acorde con la física de la luz en el experimento. Con nuestros datos, obtenemos que el coeficiente de extinción molar lineal es 1.398 ml/mg y el coeficiente no lineal es 0.524 ml2/mg2. Estos datos sugieren que, para situarnos en la zona lineal, tendríamos que haber usado concentraciones mucho más bajas, menores de 0.25 mg/ml (menores que las del tubo 1). Teóricamente, podríamos calcular la concentración a partir de la cual la atenuación es no lineal, pero es un tratamiento matemático complejo.
Usando este ajuste no lineal, obtenemos C5=0.31 mg/ml y que C6=0.49 mg/ml. De nuevo, si deshacemos la dilución, estamos muy cerca del valor real de la muestra problema. Compárese con el primer ajuste que hicimos, el lineal. Usando éste se obtienen valores muy desviados de la realidad y más altos. Idealmente, en las determinaciones colorimétricas deberíamos usuar la ley de la absorbancia polinomial, como acabamos de hacer.
Así, en las determinaciones colorimétricas es esencial tener en cuenta los efectos no lineales, para poder realizar un cálculo preciso. Idealmente, el ajuste de la ley de Lambert Beer se debería efectuar como polinomio de segundo grado.
¡gracias a Paula Herráez Torrico y Lidia Gutiérrez, de primer curso de Biología Sanitaria de la UAH, que han obtenido unos datos excepcionales en su experimento, y que hemos usado en los cálculos expuestos aquí!


