Por C. Menor-Salvan. Version 1.60. Enero 2022.
Las enzimas, proteínas con actividad catalítica, son los catalizadores más eficientes que existen. Las enzimas son capaces de aumentar la velocidad de una reacción muchos órdenes de magnitud, como por ejemplo, la ureasa, que cataliza la hidrólisis de la urea aumentando la velocidad nada menos que 1017 veces. Pero, ¿cómo pueden las enzimas catalizar tan portentosamente muchas reacciones? La respuesta a esta cuestión no es nada simple y aún quedan muchas dudas acerca de cómo las enzimas consiguen ejercer su acción. Normalmente, en libros de texto, se ofrecen explicaciones parciales o incompletas, a veces (sobre todo en los más antiguos) erróneas. Estas explicaciones no son realmente satisfactorias cuando queremos indagar en cómo es posible que una simple cadena de aminoácidos pueda ser un catalizador tan extraordinario.
A lo largo de la Historia de la Bioquímica se han propuesto diversos modelos que explicaban parcialmente aspectos de la acción enzimática. Algunos desechados ya, como el clásico modelo de ‘llave-cerradura’, así como otros más actuales, como el modelo ‘Circe’ o el modelo de ajuste inducido de Koshland, que dan una visión simplificada. Profundizar en los fundamentos de la acción de las enzimas es muy complejo, pero aun así vamos a intentar dar una visión global del tema.
Entropía y energía libre
Las funciones de estado termodinámicas entropía y energía libre son fundamentales para entender cómo funciona una enzima. La entropía es uno de los conceptos que mas dificultades crea a los estudiantes, en parte debido a que arrastran un largo historial de explicaciones parciales y simplificaciones excesivas. La entropía es una función de estado que posee cada sistema y establece cómo van a funcionar las relaciones energéticas. De modo intuitivo, siguiendo el ejemplo de Sommerfeld: ¿por qué encendemos la calefacción en invierno?. Simple: para que esté caliente. Suministramos energía a la habitación, que se disipa a través de las paredes. La energía dentro de la habitación se mantiene constante. Pero disipamos esa energía para mantener la entropía del sistema. ¿a costa de qué? a costa de un aumento de la entropía del exterior. Y ese es el drama de la termodinámica: en conjunto, la entropía del sistema (la Tierra) va a aumentar como consecuencia de nuestro esfuerzo por calentar la habitación.
Del mismo modo, necesitamos alimentarnos todos los días. Con ello disipamos una gran cantidad de energía, que disminuye la entropía de las células a costa de aumentarla en el exterior. Porque, y esta es la clave del segundo principio de la termodinámica, la entropía de un sistema sólo puede crecer.
Boltzmann nos enseñó otra visión profunda de la entropía: está directamente relacionada con el número de posibles estados energéticos de los componentes del sistema, o también está relacionada con los grados de libertad de éstos los componentes. Lo primero que hay que olvidar es la idea de que la entropía se relaciona con el desorden. Este mantra, que solía enseñarse en la Secundaria, no es totalmente incorrecto, pero da una idea confusa y es una simplificación excesiva que va a dificultar la comprensión del funcionamiento de la vida y de las enzimas. De hecho, la entropía es generadora de orden (y aquí entraríamos en una discusión mucho más compleja, pero que es la base del origen de la vida celular). Realmente, la entropía nos habla de cómo se distribuye la energía entre los componentes de un sistema. De un modo coloquial, podemos decir que cuanto más se «esparce» la energía, mayor es la entropía. Y la energía siempre va a tender a «esparcirse», por eso, globalmente, la entropía siempre crece. Piensa, por ejemplo, en una placa metálica caliente rodeada de aire frío. ¿qué es más probable, que la placa quede caliente indefinidamente, o que esa energía acumulada en la placa se «esparza» por el aire circundante?.
Veamos esta relación entre entropía y grados de libertad o estados de los componentes del sistema con un ejemplo clásico del Lehninger:
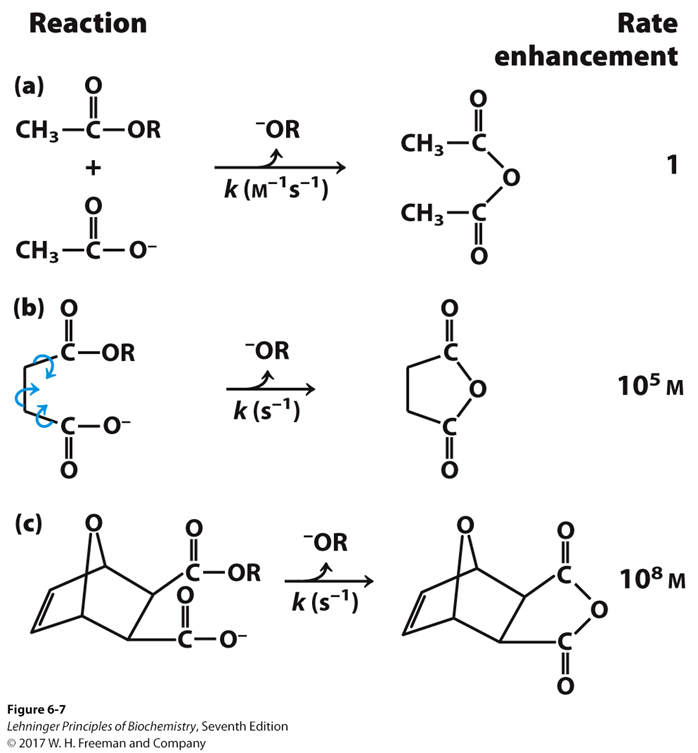
Tenemos tres reacciones (a, b y c) que son la misma: la formación de un anhídrido a partir de un éster y un ácido carboxílico. En el caso (a) tenemos dos moléculas separadas, en el caso (b) tenemos una sola molécula en cuyos extremos se encuentran los grupos reactivos, y en caso (c), lo mismo, pero tenemos una molécula más rígida. Si la velocidad de la reacción (a) es 1, vemos que la (b) es cinco órdenes de magnitud más rápida, y la (c) 8 órdenes de magnitud más rápida. Si la reacción, en realidad, es la misma, ¿Qué ha ocurrido?
En el caso (a) la entropía del sistema es mayor, porque tenemos dos componentes separados y (como dijo Boltzmann), el número de estados energéticos posibles de dos moléculas separadas es mayor. Dicho de otra forma, dos moléculas separadas tienen más grados de libertad que si las unimos: podemos distribuir la energía de más formas en el caso (a) que en los casos (b) y (c). O sea, que en el caso (a) podemos «esparcir» mucho más la energía que en los otros.
Ya vemos que la entropía no tiene que ver con el orden, sino con las posibles formas en las que podemos distribuir la energía entre los componentes del sistema. Para que tenga lugar la reacción, necesitamos que las moléculas de los reactivos estén en un estado concreto (orientación, proximidad, solvatación).
En el caso (b) ya tenemos una sola molécula. Con ello hemos disminuido enormemente los posibles estados, con lo que la entropía es menor. Ahora es más probable que se de el estado energético adecuado para la reacción de entre todos los posibles que en el caso (a). Aún tenemos muchos modos de distribuir la energía, pues los enlaces de la molécula pueden rotar, adoptando diferentes conformaciones. En el caso (c) la entropía es menor todavía, pues la rigidez de la molécula disminuye las posibilidades de generar diversos estados por rotación de los enlaces. Globalmente, hemos pagado la disminución de entropía que necesitamos para acelerar la reacción, preorientando los grupos reactivos, colocándolos en una posición bastante rígida y orientándolos adecuadamente.
Para entender esto, hay que tener clara ésta ecuación fundamental:
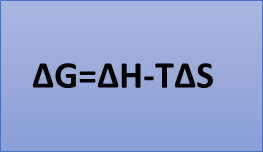
Esta ecuación relaciona la energía libre de Gibbs con la entalpía y la entropía. La energía libre nos ayuda a ver fácilmente cuando una reacción es espontánea o no.

Para que la reacción sea espontánea tenemos dos componentes: el componente entálpico (H) y el componente entrópico (S). Si una reacción tiene una variación de entalpía negativa, es decir, es exotérmica, pero requiere una reducción de entropía elevada, puede no ser espontánea. Es decir, podemos manipular la variación de energía libre de la reacción jugando con la componente entálpica, la entrópica o con ambas. Así es como actúan los catalizadores.
Hay que tener cuidado, pues que una reacción sea espontánea no quiere decir que sea rápida. ¡No hay que confundir termodinámica con cinética! y aquí precisamente es donde entran las enzimas: Una enzima no convierte en espontánea una reacción que no lo es. Lo que hace es aumentar enormemente la cinética de la reacción modificando la entalpía y/o la entropía de activación de la reacción. Un ejemplo: la oxidación de la pirita:



La oxidación de la pirita en una atmósfera con oxígeno y en presencia de humedad tiene una variación de energía libre muy negativa: es un proceso espontáneo y, además, desprende gran cantidad de energía (muy exotérmico). Esta reacción es esencial en las minas, donde puede llevar a que se produzcan temperaturas muy altas. Sin embargo, podemos tener muestras de pirita y no cambian durante años: el proceso es cinéticamente lento. De hecho, son los organismos vivos (bacterias) los mayores impulsores de la oxidación de la pirita. ¿por qué, a pesar de la variación energética tan grande, la oxidación de la pirita es tan lenta?: porque requiere superar una barrera energética para la activación de la reacción:
Cuanto mayor es la barrera, es decir, cuanto mayor es la energía libre de activación, más ‘costará’ llevar a cabo la reacción y más lenta es su cinética. Y aquí es donde entran en juego las enzimas, disminuyendo esa barrera de activación. Volvamos al ejemplo de Lehninger:

La reacción requerirá una energía libre de activación. Aunque la reacción sea espontánea en los tres casos, la energía de activación va a ser diferente dependiendo de si cambia la entalpía o la entropía de activación. En el caso (a), la entropía de activación va a ser menos favorable. Es decir, para que tenga lugar la reacción, debe reducirse más la entropía que en los casos (b) y (c). Por tanto, el factor deltaS va a ser negativo. Como el factor entrópico se resta a la entalpía, negativo x negativo es positivo, por tanto la energía libre de activación va a ser mas alta en el caso (a) que en los otros y la reacción mas lenta. Veamos ahora un modelo enzimático.
Enzimas y estado de transición: el modelo Circe y la citidina deaminasa.
Vamos a añadir un simbolito a la relación de Gibbs, de modo que tenemos ésto:
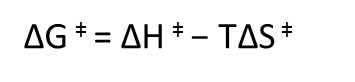
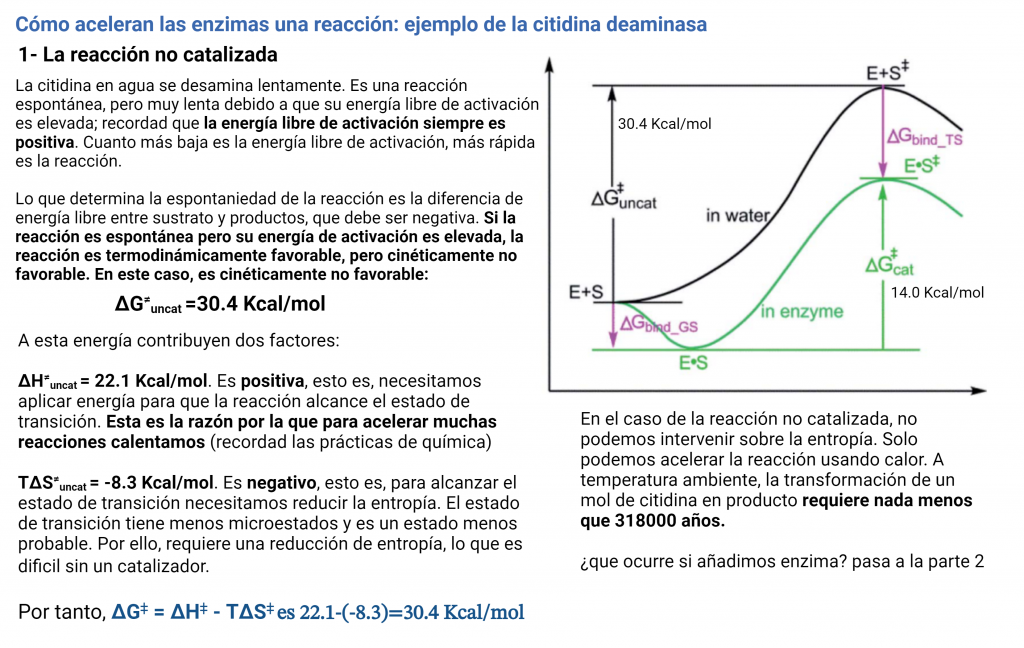
Esta es la variación de energía libre para alcanzar el estado de transición de la reacción o la energía libre de activación. Ahora vamos a ejemplificar la discusión con una reacción modelo: la desaminación de la citidina, para formar uridina. Esta reacción es espontánea y tiene lugar lentamente, simplemente disolviendo citidina en agua:
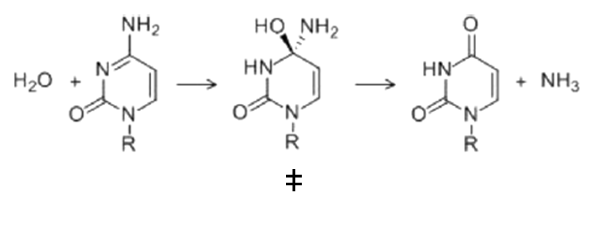
Los dos reactivos van a pasar por un estado de transición y, finalmente, formarán los productos (uridina y amoniaco). Es decir, vamos a tener una «sub-reacción» en la que el reactivo se va a transformar en el estado de transición. Para esta reacción parcial y alcanzar el estado de transición tenemos éstos valores:
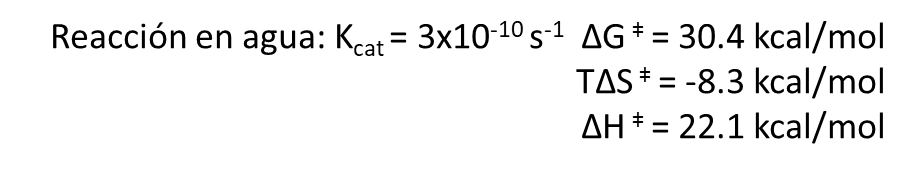
El Kcat lo veremos después, por el momento sólo vamos a fijarnos en las funciones de estado: La variación de energía libre para formar el estado de transición es positiva, lo cual quiere decirnos que la formación del estado de transición no es favorable (aunque la reacción global sí es espontánea, y por eso va a ocurrir). Para alcanzar el estado de transición, debe disminuir la entropía (el valor de -8.3 kcal/mol). Asimismo, alcanzar el estado de transición requiere un aporte de energía (entalpía positiva) como entalpía de activación. Como resultado, tenemos que la desaminación de la citidina va a progresar muy lentamente; aunque la uridina es más estable (energía libre de Gibbs más baja) que la citidina, debido a la lenta cinética, la citidina se va a mantener estable mucho tiempo. Aun así, esta reacción de desaminación es importante, ya que va a ocurrir en el DNA, donde cambios en unas pocas moléculas van a ser relevantes (pero esto es otra historia)
¿Cómo podríamos hacer para aumentar la velocidad de reacción?. Una posibilidad es calentar fuertemente: le proporcionamos la entalpía que necesita para alcanzar el estado de transición. Otra posibilidad es disminuir la entropía antes de alcanzar el estado de transición, mediante la organización, orientación y fijación los sustratos en un catalizador y generar energía para la activación mediante el establecimiento de uniones (puentes de hidrógeno y electrostáticas sobre todo) con la enzima. Y esta es una de las estrategias de las enzimas.
En una reacción catalizada enzimáticamente tenemos esta situación, totalmente distinta de las coordenadas de reacción anteriores:
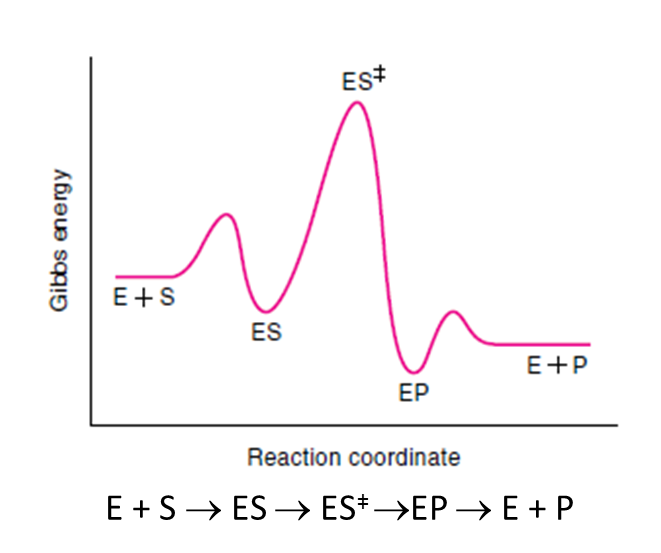
La reacción va a pasar por una fase inicial de unión de los sustratos a la enzima y formación del complejo enzima-sustrato ES. Después, llegaremos al estado de transición, la reacción progresará y se formará el complejo enzima-producto EP. Este complejo enzima-producto se disociará mucho más fácilmente, liberando el producto.
Este tipo de esquema que suele aparecer en libros de texto de enseñanza secundaria y páginas de internet:
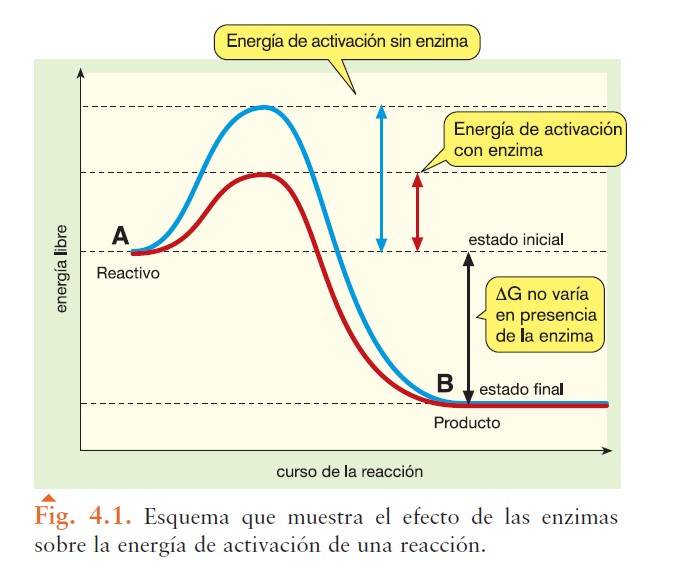
Es una simplificación incorrecta. El esquema no contempla las variaciones energéticas debidas a la formación de los complejos ES y EP y la ruptura de EP. Por tanto, mas allá de un nivel de Bachillerato, este esquema no debe utilizarse.
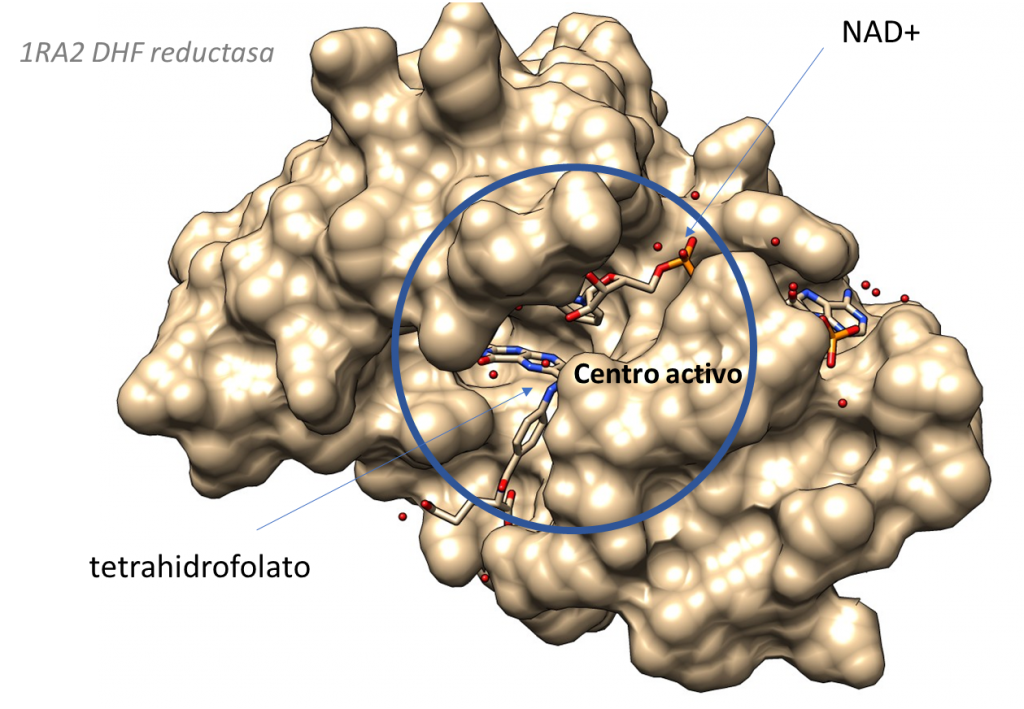
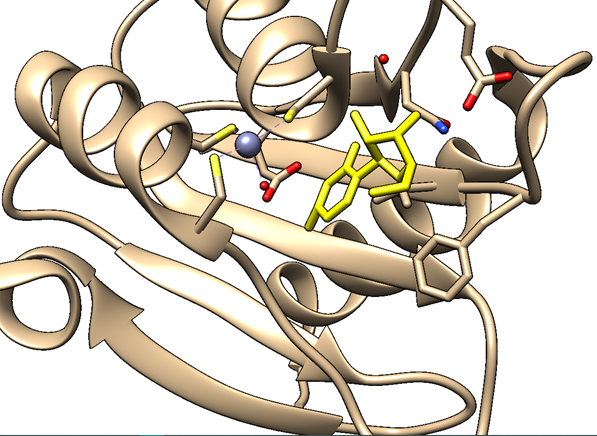
Sigamos. La siguiente figura muestra el aspecto del centro activo de la citidina deaminasa.
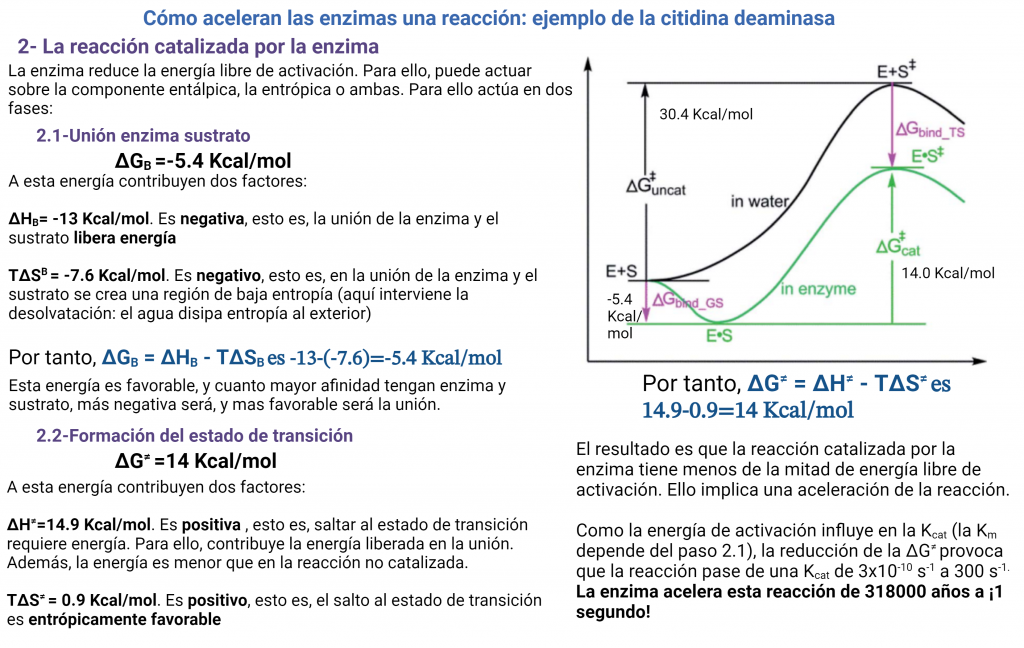
Energías en la fase de unión del sustrato a la enzima:

¿Qué significa esto? que la energía libre de unión es negativa, lo cual quiere decir que la citidina se unirá a la enzima espontáneamente. La variación de entropía en la unión es fuertemente negativa. Ello significa que en la unión del sustrato a la enzima implica reducción de la entropía. Vemos también que la variación de la entalpía es negativa, es decir se va a liberar energía en forma de entalpía de unión. Esta energía liberada en la unión va a «pagar» el impuesto entrópico e impulsar la reacción por la ‘cuesta hacia arriba’ hacia el estado de transición. Esta energía tiene varias fuentes, como la formación de interacciones (puentes de hidrógeno, electrostáticas) entre sustrato y proteína, y la desolvatación del sustrato. La energía de unión liberada es tan alta, que va a compensar la gran entropía negativa que se requiere.
Una vez estabilizado el complejo ES, tiene lugar la formación del estado de transición, con estas energías:
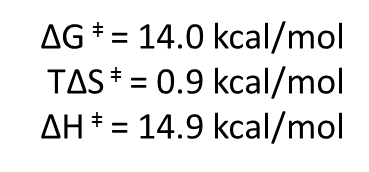
Vemos que la formación del estado de transición sigue sin ser favorable, pero ahora tenemos un valor de 14 kcal/mol, mucho mas bajo que las 30 kcal/mol que requiere la reacción no catalizada. Es decir, la enzima ha disminuido la variación de energía libre necesaria para formar el estado de transición (o energía libre de activación). Ello va a provocar un aumento de velocidad de la reacción.
Igualmente, la entalpía ha disminuido y, muy importante, la variación de entropía, positiva y próxima a cero, en la formación del estado de transición favorece la reacción. Ya pagamos el «impuesto entrópico» en la unión a la enzima, por lo que ahora no necesitamos disminuir la entropía. Esto implica que la energía generada en la unión va a impulsar la formación del estado de transición sin más impedimentos.
La enzima actuará aquí adaptándose a la estructura del estado de transición, estabilizándolo, por el que mostrará un aumento de afinidad (mayores fuerzas de atracción, con puentes de hidrógeno y electrostáticas). Esta estabilización del estado de transición implica la disminución de la entalpía de activación respecto de la reacción no catalizada, que ha pasado de 22.1 a 14.9 kcal/mol.
Vamos a resumir todo esto en forma de figuras:
La afinidad de la enzima por el estado de transición es la base del diseño de numerosos inhibidores competitivos. Es un principio general de la actividad enzimática que el centro activo de la enzima muestra mayor afinidad por la unión al estado de transición que al sustrato. Este principio es clave para la disminución de las energías de activación. Hay excepciones a éste principio, pero se cumple tan bien que es la base de una parte de nuestro arsenal de fármacos.
En resumen, en la acción de la enzima tenemos un efecto entrópico y otro entálpico, ambos dependientes de factores como la unión del sustrato al centro activo, la estabilización del estado de transición por ajuste de la enzima (que no es una estructura rígida) y optimización de la interacción, la exclusión o preorganización de las moléculas de agua en el centro activo. El efecto entrópico es la entropía de activación positiva o próxima a cero y el efecto entálpico es la disminución de la entalpía de activación debido a la adaptación y afinidad de la enzima por el estado de transición, que lleva a una estabilización de éste.
Kcat y velocidad de reacción
La constante Kcat se denomina turnover number o número de recambio. Es un indicador de la velocidad de la reacción: son los moles de sustrato que puede convertir en producto un mol de enzima en una unidad de tiempo en condiciones de saturación. La reacción catalizada por la citidina deaminasa tiene un Kcat = 300 s-1 Es decir, la enzima puede convertir 300 moles de citidina en uridina por mol de enzima y por segundo. En las mismas condiciones, la reacción no catalizada tendría un Kcat = 0.00000000003 s-1. Es decir, que para hidrolizar la misma cantidad de sustrato que la enzima es capaz de transformar en un segundo, harían falta unos ¡318000 años!. Esto da idea de la capacidad de las enzimas como catalizadores.
El numero de turnover se relaciona con la famosa constante de Michaelis-Menten. El cociente Kcat/Km se denomina constante de especificidad y se utiliza como indicador de la eficiencia de la enzima como catalizador. Esta constante tiene un máximo teórico de aprox. 108 m-1s-1, que tendría una enzima teóricamente perfecta.
El modelo Circe es una simplificación: la importancia del mecanismo
Las cuentas energéticas que hemos expuesto antes llevaron al bioquímico norteamericano William Jencks a enunciar el modelo Circe en los años 1970: La unión del sustrato a la enzima lleva a la reducción de entropía necesaria para impulsar la reacción y a la «preparación» de los enlaces del sustrato para la reacción (por debilitamiento de algunos enlaces, y por efectos de orientación). Durante la unión, enzima y sustrato se adaptan el uno al otro, se debilitan los enlaces clave en el sustrato, y se colocan y alinean los grupos químicos de la molécula, favoreciendo la reacción. Circe hace referencia a un personaje mitológico que aparece en la Odisea: la diosa hechicera Circe, que era capaz de transformar a los hombres en animales con su varita mágica, entre otros poderes. En cierto modo, la enzima es como el palacio de Circe en la mítica isla de Eea y el sustrato es Ulises, que, convencido por Circe, se queda un año con ella (lo cual fue complicado de explicar a su esposa Penélope a su vuelta a Ítaca, y hubo bastante salseo con el tema).

El problema de esta visión basada en la reducción de entropía por unión del sustrato es que es una simplificación excesiva. En realidad, la clave es que, en muchos casos, la enzima tiene un mecanismo de reacción diferente a la reacción no catalizada. Es decir, los cambios energéticos se deben a que la enzima induce otro camino de reacción más favorable.
En nuestro modelo de la citidina deaminasa, la alta entropía negativa que veíamos en la activación de la reacción no catalizada se debe a la organización de las moléculas de agua en torno a la molécula en el estado de transición. En la reacción catalizada, vemos que la citidina deaminasa es una metaloenzima que requiere de un átomo de zinc. El zinc forma un complejo con la molécula de agua y el residuo glutámico 104. Este complejo permite una reacción de transferencia de protón desde la molecula de agua, formandose hidroxilo, con un cambio de entropía positivo, favorable para la reacción. Esto es posible porque el centro activo excluye el agua, disminuyendo el numero de componentes y estados en los que puede distribuirse la energía: disminuye la entropía (a costa de un gasto energético y de aumentar la entropía del exterior). El modelo Circe simplifica el modelo, pues tanto la variación de entalpía como de entropía no se deben únicamente a la unión al sustrato, establecimiento de interacciones y exclusión del agua, sino a que el mecanismo de la reacción ha cambiado en el centro activo de la enzima respecto a lo que ocurría en agua. Ello se traduce en unas «cuentas energéticas» diferentes.
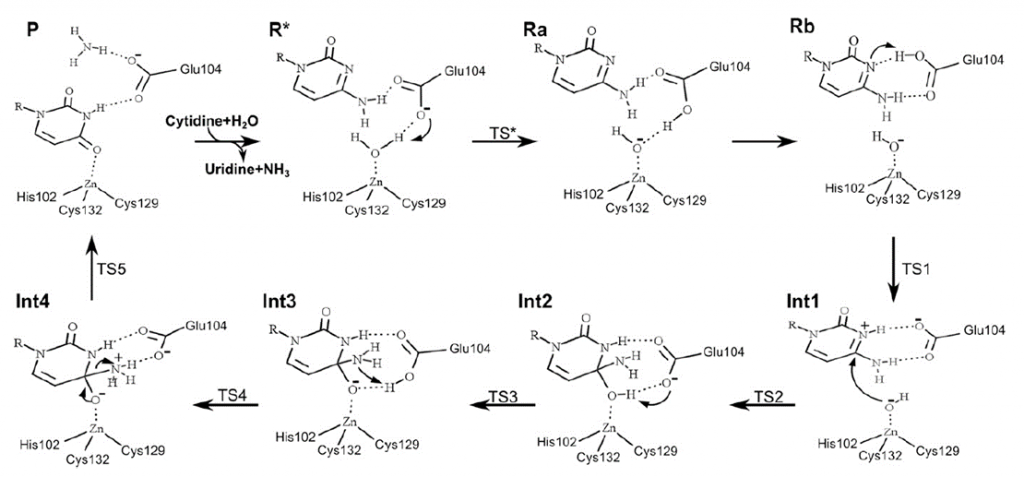
El estudio de los mecanismos de catálisis enzimática nos muestra que los efectos de proximidad, restricción del movimiento del sustrato (es decir, reducción del número de posibles estados energéticos) y orientación y estabilización del sustrato en el estado de transición, inducidos por el enzima son complementarios con el efecto entrópico debido a la solvatación y reorganización del entorno de grupos cargados, que es totalmente distinta en la reacción enzimática y en la reacción no catalizada.
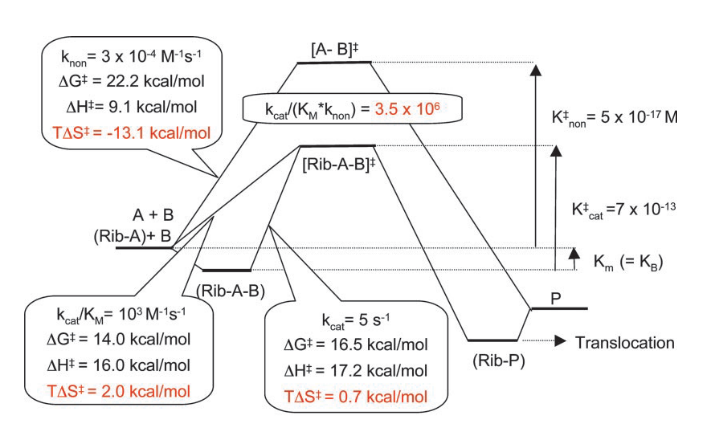
Una trampa de entropía: la peptidil transferasa
La síntesis de péptidos en la célula tiene lugar en el ribosoma, catalizada no por una enzima, sino por un RNA catalítico o ribozima: la peptidil transferasa. La peptidil transferasa no actúa como un catalizador químico normal. Es decir, no se produce un efecto entálpico de reducción de la energía de activación debido a la formación de interacciones con el catalizador. El efecto catalítico del ribosoma se debe a un efecto puramente entrópico. Decimos que el centro peptidil transferasa es una trampa de entropía.
La entropía de activación de la reacción catalizada por el ribosoma es de 2 kcal/mol, una entropía positiva, lo que va a favorecer la reacción, frente a la entropía de -13.1 kcal/mol que tiene la reacción no catalizada. Esta entropía positiva tiene dos componentes. La entropía de activación próxima a cero (0.7 kcal/mol) desde el complejo ribosoma-sustrato al estado de transición, lo que es clave en la activación, y una entropía positiva en la formación del complejo ribosoma-sustrato, lo cual es inesperado. Aquí no se cumple el modelo Circe.
En cambio, si vemos la entalpía de activación, tenemos 16 kcal/mol en la reacción catalizada frente a 9.1 en la no catalizada. Es decir, la reacción catalizada por el ribosoma requiere incluso mas entalpía (calor), al revés de lo que se esperaría en una enzima normal. Por tanto, la base de la acción catalítica del ribosoma es una entropía de activación favorable. Contrariamente a lo que veíamos con el modelo Circe, esta entropía favorable no proviene de una disminución de entropía en la unión del sustrato, sino que se origina por la preorganización y la exclusión de agua del centro activo. Este efecto catalítico es posible debido a que la reacción no catalizada en agua tiene una penalización por entropía elevada, porque requiere la reorganización de la estructura de moléculas de agua en torno al estado de transición. La «trampa de entropía» elimina este proceso de reorganización, además de colocar a los sustratos en la posición adecuada para favorecer la reacción. Fijaos, además, que aquí la ordenación del sustrato en el centro activo implica un aumento de entropía: el establecimiento de una estructura compleja es entrópicamente favorable. ¿viola el segundo principio de la termodinámica? pues no.
¿Cuánto mejora el ribosoma la velocidad de la reacción? En el caso de la peptidil transferasa, los cálculos son algo mas complicados debido a que es una reacción de segundo orden y no vamos a entrar a discutir todos los detalles. Pero como resultado, la diferencia en la entropía provoca que el ribosoma aumente la velocidad de formación del enlace peptídico nada menos que ¡3.5 millones de veces! (ver el esquema anterior). Desde luego, la entropía es muy importante.
Globalmente tenemos dos situaciones para favorecer la entropía de activación: reducir la entropía en la unión del sustrato al centro activo, posibilitando la formación del estado de transición con una variación de entropía próxima a cero (modelo Circe), o bien crear una trampa de entropía al excluir el agua del centro activo eliminando la necesidad de la reorganización de las moléculas de agua en el estado de transición, que tiene un alto coste entrópico.
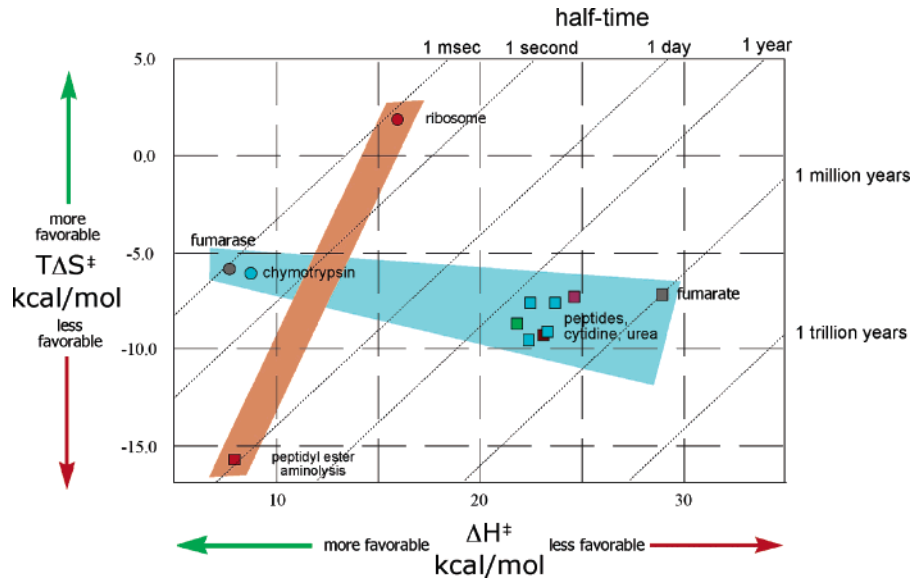
En este esquema se ilustran los dos grandes modos de acción enzimática que no se explican sólo con el modelo Circe. En la zona roja, la reacción catalizada por el ribosoma (punto rojo) aumenta su velocidad creando una trampa de entropía favorable, de modo que pasamos de una vida media (periodo para que la concentración de reactivos se reduzca a la mitad) de 1 día para la reacción no catalizada a 1 milisegundo para la reacción catalizada. Por otro lado, en la zona azul, tenemos otra reacción: la hidrólisis de péptidos, citidina, fumárico y urea (cuadrados a la derecha). La hidrólisis no catalizada presenta una vida media de entre un millón de años y un año. La acción de las enzimas fumarasa o la quimotripsina (hidrolisis de fumárico y de péptidos) reduce la vida media a 1 milisegundo. La acción de estas enzimas hidrolíticas se basa en, fundamentalmente, reducir la energía libre de activación mediante una entalpía de activación más favorable, siendo el componente entrópico menos significativo.
En conclusión, la acción de la enzima se basa en la reducción de la energía libre de activación mediante una combinación de efectos entrópicos y entálpicos. El modelo Circe, que nos dice que el ajuste del sustrato y la enzima conlleva una reducción de entropía que impulsa la reacción, es incompleto, aunque nos permite hacernos una idea de cómo funciona la termodinámica de las enzimas. El conocimiento de los mecanismos enzimáticos lleva a que las enzimas pueden tener diferentes fundamentos en su acción de mejora de la energía libre de activación.
Referencias
Åqvist, J., Kazemi, M., Isaksen, G. V. and Brandsdal, B. O. (2017) ‘Entropy and Enzyme Catalysis’, Accounts of Chemical Research, 50(2), pp. 199–207. doi: 10.1021/acs.accounts.6b00321.
Cuesta, J. (2006) ‘La entropía como creadora de orden’, Revista española de física, 20(4), pp. 13–19.
Kazemi, M., Himo, F. and Åqvist, J. (2016) ‘Enzyme catalysis by entropy without Circe effect’, Proceedings of the National Academy of Sciences of the United States of America, 113(9), pp. 2406–2411. doi: 10.1073/pnas.1521020113.
Mulholland, A. J. (2016) ‘Dispelling the effects of a sorceress in enzyme catalysis’, Proceedings of the National Academy of Sciences of the United States of America, 113(9), pp. 2328–2330. doi: 10.1073/pnas.1601276113.
Schroeder, G. K. and Wolfenden, R. (2007) ‘The rate enhancement produced by the ribosome: An improved model’, Biochemistry, 46(13), pp. 4037–4044. doi: 10.1021/bi602600p.
Sievers, A., Beringer, M., Rodnina, M. V and Wolfenden, R. (2004) ‘The ribosome as an entropy trap’, Proceedings of the National Academy of Sciences, 101(21), pp. 7897–7901. doi: 10.1073/pnas.0402488101.