¿Por qué el número de la suerte es el 7?. Sobre dados, entropía, vida y orden.

C. Menor-Salván. UAH. Actualizado Octubre 2023

El concepto de entropía y su relación con la Bioquímica es uno de los más complicados de entender por parte de los estudiantes. En este artículo, vamos a tratar, sin entrar en formalismos matemáticos, de aclarar el concepto de entropía, el significado del Segundo Principio de la Termodinámica y la relación con la vida y el metabolismo.

Introducción: Entropía NO es desorden

El concepto de entropía, una de las funciones de estado termodinámicas (es decir, una función que describe las características térmicas y energéticas de un sistema), es uno de los que más dificultades presenta para su comprensión. En mi enfoque de la enseñanza de la Bioquímica, la entropía tiene un papel esencial, pues es una de las claves que explican la propia vida y sus estructuras. La entropía es esencial para entender el funcionamiento de las enzimas y para entender por qué el metabolismo no es una colección de reacciones diseñada para fastidiar a los estudiantes, sino que tiene una lógica comprensible.

Una de las razones por las que los estudiantes tienen dificultades con el concepto de entropía es debido a una simplificación confusa que se transmite constantemente en la enseñanza: que la entropía es una medida del desorden. Mayor desorden=mayor entropía. En un texto de 2º de Bachillerato he podido leer:

La entropía S es una magnitud que mide el grado de desorden de un sistema físico o químico

Esta definición es errónea. Además suele acompañarse con imágenes como esta:

¿cómo puedo explicar a los estudiantes que la entropía es generadora de orden, y que el orden o estructura biológica es resultado del incremento de entropía, si previamente les hemos engañado con una simplificación errónea?.

Tratando de hacerlo lo más simple y conceptual posible y sin entrar en las matemáticas de la Termodinámica formal, vamos a buscar alternativas que nos permitan acercarnos al significado de la entropía y a entender por qué la entropía genera el orden biológico. Ello es necesario para entender, a su vez, por qué el metabolismo es tal como es.

Dados y estados: buscando otras analogías para entender la entropía

¿sabes por qué el 7 es considerado un número de suerte?. ¿si lanzas DOS dados, crees que hay la misma probabilidad de que salga cualquiera de los resultados posibles (la suma de lo que sale en cada dado)?. Hagamos el experimento: si lanzamos dos dados, el resultado puede ser desde 2 hasta 12. Si los lanzamos muchas veces (he estado una tarde de sábado haciéndolo), obtendremos una distribución como esta:

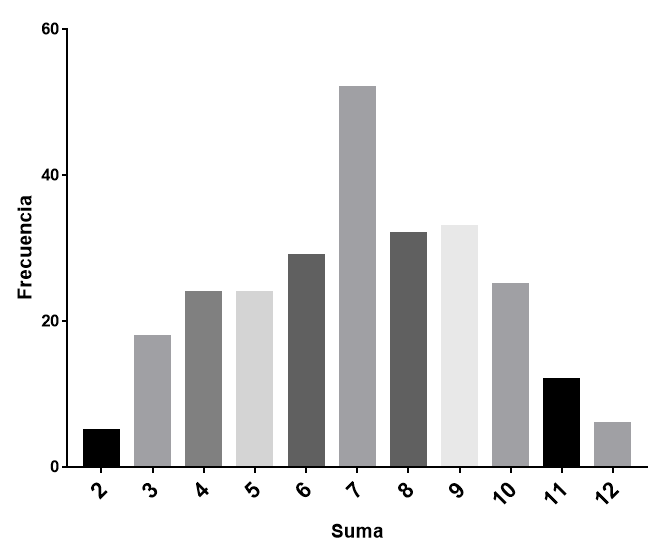
Según esta distribución, el 7 es el número mas probable. La razón de la preferencia por el 7 en el lanzamiento de dos dados es, en realidad, bastante obvia. Podemos usarla como una analogía del concepto de entropía: la probabilidad de obtener el número 7 es la mayor, por lo que el número 7 es el estado de mayor entropía. 2 y 12 representan los estados de mínima entropía, razón por la cual son las apuestas mas arriesgadas. Antes de explicar por qué es así, vamos a dejarnos enseñar por el físico aleman Arnold Sommerfeld.

La definición (algo más) formal de entropía.

Sommerfeld explicaba en 1938 lo siguiente:

¿por qué encendemos una estufa en invierno [igual este invierno lo vamos a tener difícil…]. Una persona común dirá: para que la habitación esté mas caliente; un físico se expresará hablando de suministrar energía. En este caso, tendrá razón el profano y no el físico

Según Sommerfeld, este ejemplo lo proponía el físico suizo Robert Emden. El caso es que, en efecto, encendemos la estufa para que la habitación esté caliente. Este calor se disipa constantemente a través de las ventanas y las paredes; por ello si apagamos la estufa, la temperatura comienza a disminuir. Aquí no os estoy descubriendo nada nuevo.

Como la habitación es mayoritariamente aire, sabemos que la energía contenida va a depender de la temperatura. Esto se expresa a través de esta ecuación:

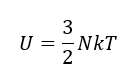
Esta ecuación nos dice que la energía U contenida en la habitación es proporcional al número de átomos que hay en la habitación, N, y a la temperatura de la habitación, T. Parece lógico: cuanta más temperatura, más energía.

También sabemos que, si calentamos un gas, va a sufrir o un aumento de presión o una expansión. Como en la habitación la presión va a ser constante, mantener la temperatura constante implica que vamos a mantener constante la energía contenida en la habitación. Pero, mientras la estamos calentando, el aire se va a expandir, saliendo por las rendijas e intercambiándose con el exterior.

¿qué ocurriría si la habitación estuviera perfectamente aislada? Lógicamente, al no poder expandirse, aumentaría la presión y la temperatura. Pero, una habitación normal es un sistema abierto, es decir, puede intercambiar energía con el exterior, y también materia, pues hay intercambio de aire a través de rendijas. Por lo que el aislamiento perfecto no va a existir.

Rudolf Clausius nos explicó que la variación de entropía de un sistema es el cociente entre el calor suministrado dividido entre la temperatura. Es decir, la entropía no es una medida de desorden, sino una medida de la relación entre energía suministrada y temperatura.

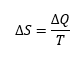
Como queremos mantener nuestra habitación a temperatura y presión constante (no queremos morir, y hay rendijas, por lo que el aire puede expandirse), hemos deducido, a partir de la ecuación anterior y de las propiedades de los gases, que a presión constante, la variación de entropía en nuestra habitación es:

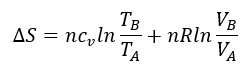
Es decir, que la variación de entropía que tenemos en la habitación es proporcional al incremento de la temperatura desde A a B, y al incremento de volumen del aire desde A a B. Si aumentamos la temperatura, entonces, aumentamos la entropía. n es el número de moles de aire, y cv es el calor específico. Idealmente, una vez que hemos alcanzado una temperatura constante, ya no hay aumento de entropía. Y por tanto, no sería necesario suministrar más calor. Observad que no hablo de orden. El incremento de entropía va asociado al incremento de temperatura y/o volumen. Las moléculas del aire ¿están igual de ordenadas o más ordenadas?. No lo se. Pero si sabemos que, si aumentamos el volumen, por ejemplo, al calentar, les estamos dando a nuestras moléculas más libertad para moverse. Vamos a volver a esta idea de ‘libertad’ más adelante.

Pero, en nuestra habitación ocurre un proceso irreversible: el calor se disipa al exterior de dos formas: irradiándose a través de los materiales y las ventanas, y mediante intercambio de aire caliente del interior con aire frío del exterior.

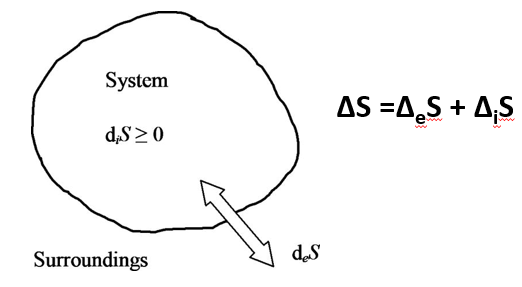
El intercambio de materia y energía de la habitación (nuestro sistema) con sus alrededores, implica que tenemos que descomponer la entropía en dos términos: Δ_iS es la entropía generada en el interior de la habitación, que es siempre cero o positiva; Δ_eS es la entropía del proceso de intercambio con el exterior y puede ser negativa, cero o positiva. Como la entropía es el cociente entre calor y temperatura, y queremos mantener la temperatura y presión constante en la habitación, entonces:

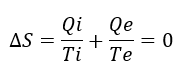
La temperatura del exterior de la habitación Te es menor que la temperatura del interior Ti. Por tanto, si perdemos todo el calor, o sea, Qi=Qe, entonces el término de entropía de intercambio con el exterior es mayor en valor absoluto. Como el intercambio con el exterior está sacando calor de la habitación, entonces, el término es negativo. Por tanto, la variación global ΔS=Δ_iS–Δ_eS<0. Hemos visto antes que la entropía depende de la temperatura, por lo que si sacamos el mismo calor que metemos, la habitación se enfría hasta que Ti=Te. Esto es lo que ocurre en una habitación cualquiera: en el momento que apagamos la calefacción, la habitación se enfría. Al final, Qi se igualará con Qe. La clave para mantener la habitación caliente es suministrar energía constantemente y llegar a un estado estacionario en el que Qi>Qe durante un lapso de tiempo.

Total, que para mantener la temperatura constante, y, por tanto, ΔS=0, necesitamos que Qi>Qe, es decir, suministramos más energía de la que perdemos durante el tiempo que queremos estar calientes. Lógico, ¿no?. Por ello nos interesa minimizar Q_e, utilizando aislamientos, de modo que podamos minimizar Q_i, y reducir la factura de la luz. Aquí voy a añadir una nota: estamos simplificando mucho la discusión, pues nos estamos centrando en el aire, un gas, y además lo consideramos un gas ideal. Cuando hablemos de reacciones químicas, cambios de fase, etc. la discusión se complica, y hablaremos de energía libre, entalpía y entropía.

El término Δ_eS negativo lo denominó Schrödinger entropía negativa o neguentropía: la entropía asociada al proceso de disipación. Es decir, estamos neutralizando la acumulación de entropía en la habitación al calentarla, sacándola fuera y aumentando la entropía del exterior.

Esto es lo que define el SEGUNDO PRINCIPIO DE LA TERMODINÁMICA: la entropía total del universo (nuestra habitación + el exterior) siempre aumenta. Por ello, para poder mantener la entropía de la habitación constante (que mantenga su temperatura y presión constantes) necesitamos estar constantemente generando calor en ella y aumentar la entropía del universo.

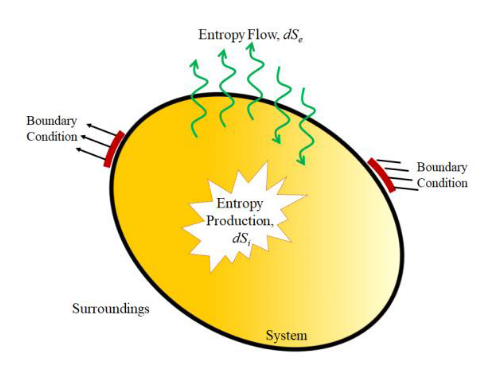
Con esto hemos explicado físicamente lo que todos sabemos por experiencia: que si apago el radiador, la habitación se enfría. Por este principio, los ingenieros han hecho enormes esfuerzos en reducir los procesos irreversibles en máquinas y edificios, tales como reducir la disipación de calor mediante aislamiento, disminuir el rozamiento y desgaste en los motores, etc. En la vida real, como vamos a tener procesos irreversibles, siempre tenemos que consumir energía para ‘pagar’ esta especie de impuesto entrópico. Esta es la razón por la que no existe el móvil perpetuo y por la que, hagamos lo que hagamos, siempre se va a enfriar la casa al apagar la calefacción.

Aplicación en la bioquímica

La discusión anterior se puede aplicar exactamente igual a un organismo vivo, ya sea una célula o un animal.

En 1992 se publicó un interesante experimento: los investigadores midieron, usando un calorímetro, la producción de entropía de cerditos en una granja y observaron que la producción de entropía iba creciendo durante el periodo infantil, hasta alcanzar un máximo. Cuando el cerdito entraba en edad adulta y cesaba su desarrollo, la producción de entropía disminuía, e iba disminuyendo gradualmente hasta la vejez.

Es decir, mientras estaba en proceso de morfogénesis activa, generando estructura biológica, la disipación de entropía crecía. En la edad adulta entra en estado estacionario.

La ecuación que vimos antes:

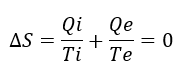
la podemos expresar así:

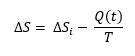
En la que la velocidad o la variación de la producción de entropía es el balance entre la producción de entropía interna del sistema (es decir, debida al metabolismo y procesos vivos del cerdito) y la disipación de energía al entorno en forma de calor (Q) que es una función que varía con el tiempo (estamos en un sistema dinámico), en relación con la temperatura del sistema. Aquí, el calor Q no hay que confundirlo con temperatura. El calor engloba la irradiación de energía y la disipación de energía transportada por moléculas, como el agua, CO₂ y otras moléculas emitidas por el organismo, que ‘esparcen’ o ‘dispersan’ la energía. En estado estacionario, ambos términos se igualan.

Por el contrario, si la tasa de producción interna de entropía es menor que la disipación de calor, la variación de entropía es negativa. Tenemos la ‘neguentropía’ y, en el proceso, es cuando se produce la auto-organización de las estructuras de los organismos vivos.

Ilya Prigogine entra en escena: explicando la vida con el teorema de mínima entropía, sistemas no lineales y estructuras disipativas.

Resulta que estamos disminuyendo la entropía de nuestro sistema, mediante la disipación de energía y el aumento de entropía del exterior del sistema. Hay varios tipos de este sistema peculiar que, espontáneamente, se ha alejado del equilibrio.

Uno de estos sistemas es el metabolismo.

El metabolismo es un conjunto conectado y coordinado de reacciones químicas que permite, según el teorema de mínima entropía de Prigogine, minimizar la entropía producida durante la disipación de energía libre, maximizando la negentropía. Ello lleva a la reducción de entropía interna del sistema y la aparición de estructuras emergentes. Este tipo de sistemas se denominan estructuras disipativas (mas adelante volveremos a este concepto).

El metabolismo permite que los organismos vivos se ‘alimenten de entropía negativa‘ (como expresó Schrödinger). Este concepto aún está en discusión y también se ha sugerido que la evolución marca un camino hacia la maximización de la producción de entropía, provocando un aumento de complejidad que aumente la neguentropía para mantener la estabilidad dinámica. En fin, aquí entramos en un área muy compleja. Tanto que lo llamamos la Ciencia de la Complejidad. Pero como sumario, podemos decir que hay una diferencia fundamental entre un sistema vivo y una máquina: en las máquinas, los ingenieros quieren reducir los procesos irreversibles para aumentar su eficiencia disminuyendo la entropía. En la vida, en cambio, DEPENDE de los procesos irreversibles y la producción de entropía es la que hace que funcione. ¿por qué depende de ellos? porque la vida surge a costa de alejarse del equilibrio y de aumentar la disipación de entropía (el segundo término en la última ecuación)

Un ejemplo relativamente simple de estructura disipativa, muy similar al metabolismo, es la reaccion de Belousov-Zhabotinsky:

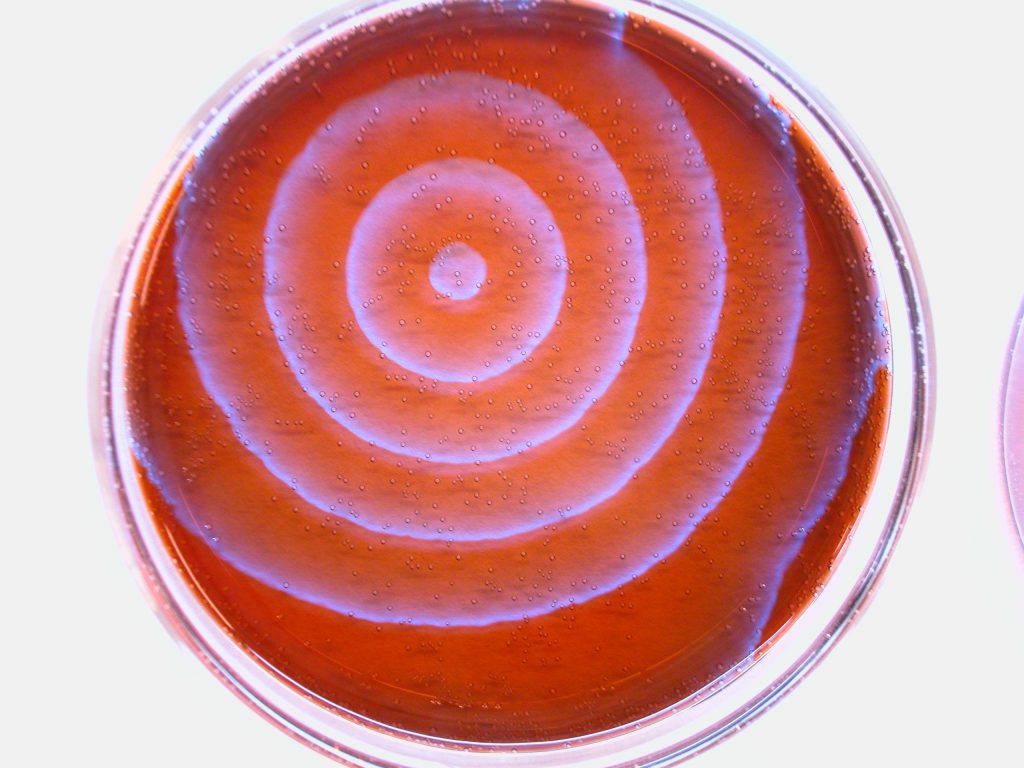
La aparición espontánea de patrones durante la reacción, como los de la imagen, que son zonas con diferentes parámetros físicos y químicos, es resultado de la disminución de entropía, mediante la transformación de la energía contenida en el ‘combustible’ de la reacción y el aumento de entropía del exterior. Es una estructura disipativa que depende del aumento de entropía del exterior. Por ello, una estructura disipativa, tal como el metabolismo, sólo puede producirse en un sistema abierto. En un sistema cerrado en el que no pueda intercambiar materia y energía con el exterior, el sistema ‘muere’ rápidamente.

¿qué tienen en común la reacción de Belousov con el metabolismo? Para que un sistema químico tenga estas propiedades, deben establecerse una serie de ciclos y reacciones encadenadas, en los que se alternen reacciones químicas reversibles e irreversibles y se produzca un fenómeno de autocatálisis o de catálisis recíproca. Aquí ya entramos en una complejidad excesiva (alguien pillará el chiste), por lo que lo dejamos en éste punto. Pero, la idea es que para que se de la vida tal como la conocemos, el metabolismo tiene que ser tal como es, y debe contener un sistema de reacciones como la glucólisis, que hacen posible que la disipación de entropía permita formar las estructuras biológicas.

Alguien podría preguntar: entonces, termodinámicamente, ¿la reacción de Belousov es vida?. No. La diferencia fundamental es que un organismo vivo es capaz de regular internamente su comportamiento estructural. La estructura en la reacción de Belousov es resultado de los cambios e influencia de su entorno, sin control interno. Este control estructural y regulación interno, que está relacionado con la información biológica, es lo que llamamos biología molecular. Así, podemos establecer un criterio de demarcación entre la biología molecular y la bioquímica, si queremos.

Reacción de Belousov-Zhabotinsky: un modelo del metabolismo.

Vamos a ver de nuevo el ejemplo de la reacción de Belousov:

Belousov descubrió, en 1951, su famosa reacción tratando de encontrar un modelo de laboratorio para el metabolismo central (glucolisis+ciclo de Krebs). Lo que encontró fué fascinante: una reacción que no era ni un equilibrio ni irreversible, sino que oscilaba entre el estado inicial y el final. Si la reacción se lleva a cabo sin agitación y en una capa fina, tiene lugar la formación de bellas estructuras llamadas patrones de Turing.

Belousov estudió exhaustivamente la reacción y propuso un esbozo de su mecanismo (que tardaría décadas en resolverse); envió sus resultados y los detalles experimentales para ser publicados en una importante revista científica, en 1951. Los revisores recomendaron contra su publicación y el editor respondió a Belousov que su “supuesto descubrimiento” era “imposible”. Seguramente, la idea de que una mezcla química se comportase como un péndulo, o que en un líquido homogéneo surgieran estructuras de composición química diferenciada, violando en apariencia el Segundo Principio de la Termodinámica, pesaba más que el repetir la simple receta de la reacción y verlo con sus propios ojos. El editor dijo a Belousov que tenía que aportar más pruebas. Boris entonces volvió al laboratorio y tras otros seis años de trabajo (la Ciencia requiere tiempo…), envió un nuevo artículo, más elaborado y con un estudio profundo del mecanismo. La respuesta que recibió fue de rechazo y un escepticismo aún mayor. Ni los revisores ni los editores se molestaron en repetir por ellos mismos una reacción extremadamente sencilla de reproducir. Simplemente se dejaron llevar por sus prejuicios. Belousov, que ya tenía 64 años, estaba tan enfurecido y decepcionado que decidió no volver a publicar ningún artículo jamás ni relacionarse con otros científicos. Publicó su receta de la reacción en un simposium, quedando solo un oscuro resumen en ruso en el fondo de algunas bibliotecas.

Cuando Zhabotinsky tomó el testigo, la receta de la reacción de Belousov era conocida en diversos centros en la URSS, aunque se desconocía su autor y origen. Zhabotinsky comenzó, como tema de tesis, a estudiar esa curiosa reacción que circulaba por ahí. En los años 60, ya había realizado un extenso estudio y había descubierto al autor de la reacción original: Boris Belousov. Informó a éste de su trabajo y
progresos y Boris le remitió, muy agradecido por recuperar su vieja receta, su manuscrito rechazado original y otro material. Cuando la reacción empezó a ser conocida fuera de la URSS, a finales de los 60 y principios de los 70, aún era conocida como la “reacción de Zhabotinsky”, aunque por el
esfuerzo de éste, el crédito para Belousov fué finalmente reconocido. Zhabotinsky mantenía informado de sus progresos a Belousov, pero éste siempre rechazó un encuentro personal, así como asistir al simposio sobre reacciones oscilantes que se había organizado en Praga en 1968. Así, Zhabotinsky y Belousov nunca se conocieron personalmente. Belousov murió en 1970, sin llegar a conocer las implicaciones que tendría su trabajo ni disfrutar del reconocimiento que actualmente se le brinda.

Desde el punto de vista de la termodinámica, podemos usar la reacción de Belousov para entender cómo funciona un sistema metabólico:

En primer lugar no es una sola reacción, sino que se genera un sistema multicomponente, abierto y genera una red o ciclos de reacciones. Uno de estos ciclos es un ciclo autocatalítico en el que los productos son, a su vez, reactivos. Estas características las comparten tanto un sistema metabólico como la reacción de Belousov.

Los patrones de Turing son impredecibles, jamás son exactamente iguales y su estructura depende de pequeñas diferencias en las condiciones iniciales. Son el resultado del acoplamiento entre las reacciones químicas y los procesos de difusión. Esta relación es no lineal y da lugar a múltiples estados estacionarios, igualmente probables. La formación de las estructuras, que manifiestan los estados estacionarios, depende de las fluctuaciones microscópicas. Prigogine lo llamaba «orden a través de la fluctuación». En un sistema biológico, las fluctuaciones son cambios ambientales, epigenética o variaciones genéticas, y las estructuras son el fenotipo.

El sistema (ya sea la reacción de Belousov o el metabolismo) alcanza un estado alejado del equilibrio, en el que maximiza la disipación de energía libre de los reactivos, minimiza la producción de entropía y maximiza la disipación de entropía fuera del sistema, de modo que el sistema se sostiene con la neguentropía y, aunque la entropía global aumenta, dentro del sistema se produce una reducción temporal de entropía. En el vídeo podéis ver uno de los modos de disipación de entropía: las burbujas de CO2, el residuo que produce la reacción, y que se eliminan. Este es el principio de mínima producción de entropía de Prigogine. El sistema evoluciona reduciendo su producción interna de entropía y maximizando la disipación. Pero, la reacción de Belousov no es un buen sistema abierto, y termina acumulando demasiada entropía y «muriendo»

Otro modelo, el modelo de máxima disipación de entropía, sugiere el sistema tenderá al estado estacionario en el que la producción de entropía sea máxima. Es decir, la evolución tiende a maximizar el aumento de entropía del entorno, lo cual puede hacerse mediante el balance entre la producción interna de entropía (que siempre aumenta) y el intercambio con el exterior.

La reacción de Belousov o la vida misma no son más que disipadores de energía libre y generadores de entropía. Esto permite la evolución compleja de estructuras durante el proceso de disipación de la energía libre (nutrientes) hacia los resíduos (CO2). Prigogine las llamó estructuras disipativas.

Esto nos lleva al concepto de línea del tiempo: el proceso no se puede revertir. Percibimos el tiempo en cuanto partimos de un estado inicial de baja entropía y/o alta energía libre, para terminar en un estado que ha maximizado la entropía y ha disipado la energía libre en forma de calor. Esta es la razón por la que no se puede viajar al pasado, pues ello violaría el segundo principio de la Termodinámica; viajar al pasado implicaría moverse hacia una reducción de entropía del universo.

La vida surge, como una perturbación temporal, en el proceso de disipación de la energía y del aumento de la entropía del universo. Por ello, la vida y estructuras complejas no surgen en los estados de mínima entropía o de máxima entropía, sino de modo dinámico durante el proceso de disipación de energía y aumento de la entropía del universo.

Otro aspecto interesante de estos sistemas es la adaptación y auto-reparación. Las estructuras disipativas son estables a perturbaciones y pueden absorber éstas y ‘auto-sanarse’. La capacidad de autoreparación se puede observar en la reacción de Belousov si se introducen perturbaciones:

Vida y disipación de entropía en el planeta Tierra

Hay una idea interesante al considerar la vida globalmente: la vida surge en la Tierra como una consecuencia del teorema de la maximización de la entropía. La Tierra recibe energía del Sol y debe disiparla. Si no se disipase, el planeta se habría calentado hasta fundirse. En el proceso de disipación, surge la vida como una estructura que contribuye a mejorar esa disipación (es decir, el segundo término de la última ecuación que escribimos).

La Tierra, globalmente, constituye una gran estructura disipativa en la que:

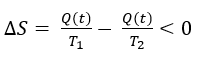
donde T1 es la temperatura de la superficie del Sol (aproximadamente 6000 K) y T2 es la temperatura de equilibrio del planeta, que es a grosso modo la temperatura a la que la Tierra irradia energía, y que es aproximadamente 300 K. Dado que la energía no se acumula en la Tierra (si así fuera, el planeta se calentaría gradualmente), el segundo término de la ecuación es aproximadamente 3×10²⁴/300 cal/grad g

La Tierra recibe mucha energía y poca entropía, es decir, energía de alta ‘calidad’, y se disipa al espacio con un flujo de entropía mucho más elevado. Ello es lo que asegura que se sostenga la vida en la Tierra. Sin embargo, esta cuenta global no es suficiente para entender cómo surgió y cómo funciona la autoorganización molecular que da la vida.

Pero, en términos globales, la biosfera funciona como ciclos de Morowitz (ver más adelante) en los que los organismos fotosintéticos capturan energía solar, la convierten en hidrógeno y genera un gradiente de potencial, que se disipa, impulsando la generación de biomasa. La energía del hidrógeno se almacena y transporta en forma de azúcares, que son utilizados por otros organismos para reconvertirlos en hidrógeno y generar un gradiente, que impulsa a su vez la generación de biomasa o la producción de entropía en estado estacionario. En cada paso, la energía solar se ‘degrada’, o se ‘esparce’, creando un eficiente flujo de entropía hacia el exterior.

La vida en el planeta no es más que otra estructura asociada al principio de máxima producción de entropía. En un planeta como la Tierra, los flujos de fluidos y energía (Sol, calor interno del planeta) han provocado la autoorganización de estructuras (incluyendo la vida) que maximizan el flujo de entropía. Esto no ocurre en todos los planetas. En el Sistema Solar, el principio de máxima producción de entropía se aplica además en Marte, Titán, Europa o Encelado. Por ello, son lugares de interés astrobiológico.

Ludwig Boltzmann, probabilidad y distribución de energía.

Obsérvese que en ningún momento hemos relacionado la entropía con una medida del orden a pesar de haber estado un rato hablando de entropía. Hemos hablado de la aparición de estructuras (como es la estructura celular), y del macroestado, es decir, el balance global de calor y la temperatura de la habitación, pero no hemos hablado de ‘orden’. Ahora ha llegado el momento de volver a los dados de nuestro juego.

Si lanzamos dos dados, la apuesta más segura es el 7. ¿Por que?. Podemos considerar el resultado de la tirada como el macroestado del sistema, que es el resultado de una serie de microestados, que definimos como el resultado de cada dado en particular (es decir, el estado termodinámico de cada componente del sistema). Al final, el estado global del sistema es el resultado de los estados particulares de cada uno de sus componentes. Por ello, en la primera ecuación hablábamos que la energía del sistema (macroestado) dependía de N, el número de átomos, cada uno de ellos en un ‘microestado’ determinado.

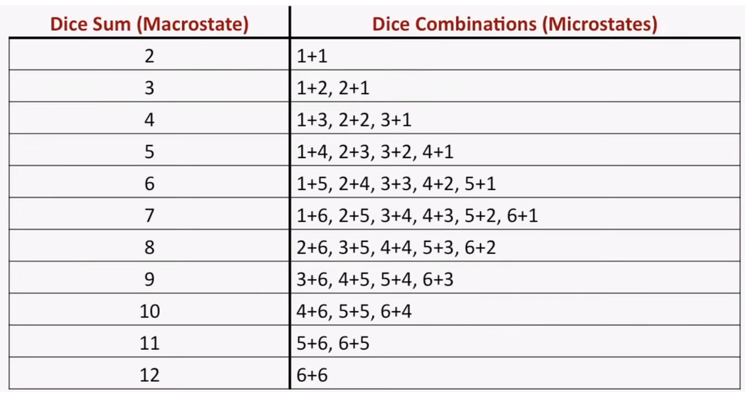
Cuantos más microestados posibles tenga un macroestado, más probabilidad tenemos de tener el macroestado resultante. Esto se llama probabilidad termodinamica. En el caso del número 7, es el macroestado resultante de seis microestados posibles. Y, lo que nos descubrió Boltzmann es que la mayor entropía tiene lugar en el macroestado al cual conducen el mayor número posible de microestados.

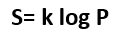
La ecuación de Boltzmann dice que la entropía es igual al producto de una constante (la constante de Boltzmann, determinada por Planck) por el logaritmo de la probabilidad de ese estado. El principio de Boltzmann nos dice entonces que el aumento de entropía en un proceso es la consecuencia de la transición del sistema del estado menos probable al más probable. En nuestro juego de dados, el estado más probable, el de mayor entropía, es el número 7, y por ello el sistema de dos dados tiene la máxima frecuencia en 7 en su distribución de estados.

Veamos otro ejemplo para ilustrar el principio de Boltzmann:

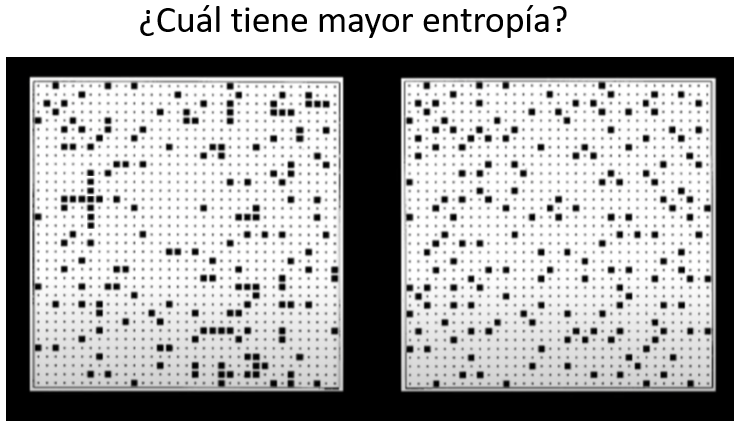
Si pregunto a los estudiantes, a los que se ha engañado con la idea intuitiva de que la entropía mide el grado de desorden, la mayoría responden que la imagen de la derecha se corresponde con el estado de mayor entropía. Pero NO. La probabilidad de que en una distribución de puntos en la cuadrícula (es decir los microestados) no haya ningún punto al lado de otro es MÍNIMA, y, de hecho, esta distribución no se ha generado al azar. Si distrubimos puntos al azar, siempre va a haber alguno pegado a otro.

El estado de la imagen de la izquierda es, por tanto, más probable, no importa cómo estén ordenados los puntos. Y es más probable, porque por azar resultan mas combinaciones de puntos (microestados) con el mismo número de contactos de unos puntos con otros. Por tanto, la imagen de la izquierda sería el estado de mayor entropía.

Entropía: una medida de la ‘utilidad’ de la energía y la burocracia como análogo

En todo proceso, hay un intercambio energético. Esta energía se invierte en hacer ‘algo’, como mover un motor, o hacer una transformación química. Esta energía que invertimos e intercambiamos la llamamos energía libre.

Pero claro, para que se produzca el proceso, hay que pagar una especie de impuesto: No toda la energía se invierte en hacer algo útil (como mover el motor o transformar moléculas), sino que una parte se «disipa» sin que haga nada de utilidad. Es el término entrópico de la energía libre.

Esta idea de ‘utilidad’ de la energía la podemos ilustrar con una analogía con la burocracia.

Todos odiamos la burocracia. En mi trabajo como profesor, la burocracia requiere una cantidad considerable de esfuerzo y dedicación. Podríamos definir la burocracia como el trabajo que no se invierte en nada productivo, pero se disipa para mantener la estructura. Como veis, volvemos a la idea de entropía como generadora de orden.

La burocracia es entropía que se genera y se disipa. En la disipación de esta entropía reside el mantenimiento de toda una estructura organizativa. Es decir, cuanto más grande y compleja es una organización, más estructura requiere mantener y más burocracia, es decir, disipación de entropía requiere. ¿como aplicamos aquí el principio de mínima producción de entropía de Prigogine?. Muy sencillo: intentamos minimizar el tiempo que dedicamos a la burocracia, maximizando la disipación de ésta. Un sistema biológico funciona de modo parecido, manteniendo así su estructura. El problema es que un sistema disipativo, ya sea un organismo, una estructura o un estado, va a depender de este proceso de generación y disipación de entropía. Ello lleva a que la complejidad vaya aumentando hasta que el sistema no es capaz de disipar más entropía de la que produce, teniendo lugar el envejecimiento y degradación de la organización.

En un estado o empresa es igual: si los requerimientos burocráticos aumentan en exceso, el sistema pierde eficiencia en la disipación de entropía que se acumula, dando lugar a la degradación de la estructura y su muerte. Todos conocemos este proceso cuando estamos sometidos a burocracia paralizante, que hace que sea muy dificil llevar a cabo tareas útiles y todas las estructuras se degradan.

La entropía: una medida de la ‘degradación’ y ‘dispersión’ de la energía

Podemos ilustrar esta idea de degradación de la energía usando una analogía: billetes y moneda fraccionaria

Si tomo un billete de 20 euros y lo cambio en 40 monedas de 50 céntimos, voy a tener el mismo valor monetario (es decir, la energía se conserva). Sin embargo, estoy «esparciendo» o «dispersando» ese valor: he aumentado la entropía (Δ_iS>0). Si yo ahora doy una moneda a cada persona que pasa por la calle, ese valor (esa energía) la he «esparcido» y la he expulsado del sistema: he aumentado la entropía del entorno, y he reducido la entropía de mi sistema (Δ_eS<0), pero a costa de pagar 20 euros. Cada persona que se ha llevado 50 céntimos, realmente poco puede hacer con ellos. Habría hecho más con los 20 euros, ¿verdad?. Es decir, con el aumento de entropía, al repartir y «esparcir» la energía, ésta se ‘degrada’.

Este proceso, en el que, globalmente, me he quedado igual que antes, pero con 20 euros menos, es un proceso cercano al equilibrio. Ahora imaginad que yo hago lo mismo, pero le pido a cada persona a la que doy una moneda que me suba una cosa que he comprado en el súper y la coloque correctamente en la cocina. Estoy estableciendo unos ciclos y la disipación de los 20 euros lleva a que surja una estructura ordenada en mi sistema. Entonces estaríamos hablando de una estructura disipativa: El empleo de energía y la disipación de entropía, generan la estructura. Imaginad que cada moneda es el CO2 que expulso en cada ‘ciclo’ metabólico, y que el billete original era la glucosa que he consumido en el proceso y tendremos una analogía para relacionar la entropía con el metabolismo. Como con las monedas, el CO2 tiene escaso valor (es una molécula muy estable y con un sobrepotencial muy elevado, que la hace poco reactiva, de ahí la dificultad para convertirla en otros materiales), comparado con la glucosa original, de la que se puede extraer bastante energía. Ahora necesitamos un sistema que recopile las monedas y las convierta de nuevo en billetes de 20 euros. Este sistema son los organismos autótrofos, que, utilizando la luz o la energía química de los minerales, fijan el CO2, convirtiéndolo de nuevo en ‘billetes’ de alto valor: los azúcares, que a su vez se transforman en otros muchos productos.

Esta idea de los ciclos la expresó Harold Morowitz en su Teorema de los Ciclos de Morowitz:

Esto nos permite definir la entropía de un modo intuitivo: es una medida de la dispersión de la energía: cuanto más dispersa, es decir, cuantas más formas tengamos de distribuir la energía entre los componentes del sistema, mayor es la entropía. Lógicamente, si en los productos de la reacción tengo mucho CO2, tengo muchas formas de distribuir la energía entre cada una de las moléculas de CO2; por tanto, tengo más microestados que se manifiestan como el macroestado, y eso aumenta la probabilidad y la entropía.

También decimos que al aumentr la entropía, aumentamos los grados de libertad del sistema. Cuantos más grados de libertad, mayor entropía. Veámoslo con un ejemplo clásico de Lehninger:

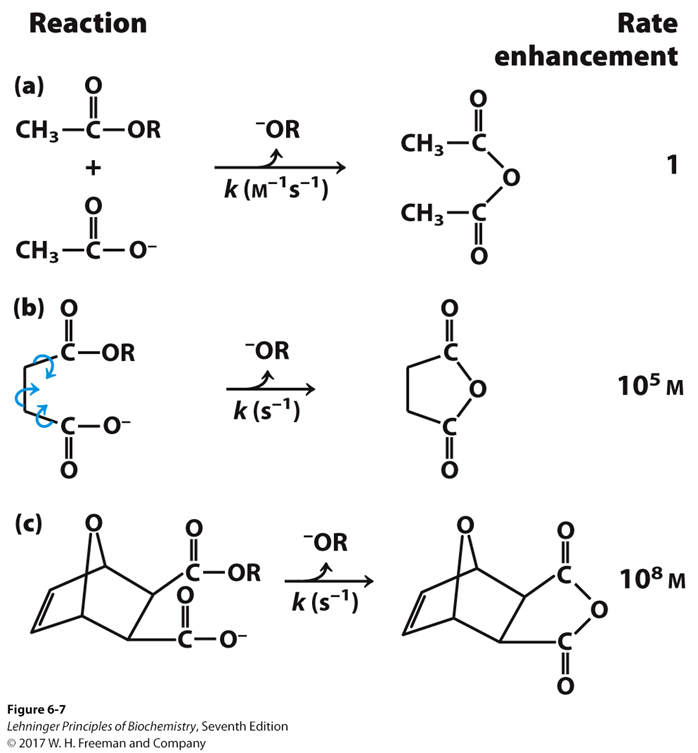
¿cual de los tres casos, a, b o c, tiene mayor entropía?. ¿puedes definirlo según el concepto de «estado ordenado» que te contaron? En el caso (a) tenemos dos reactivos separados. Podemos distribuir energía entre las dos moléculas y todas las posibles vibraciones entre sus enlaces. Tened en cuenta que, en la molécula, la energía se distribuye haciendo vibrar y rotar los enlaces, y en el caso (a) hay muchas más formas de hacerlo que en los otros (tenemos más microestados). En el caso (b) tenemos una sóla molécula, pero esta molécula tiene tres enlaces capaces de rotar completamente, con lo que tenemos más grados de libertad, es decir, más formas de distribuir la energía, es decir, más microestados, que en caso (c), en el que tenemos una molécula rígida, por lo que las posibilidades de rotaciones y vibraciones disminuyen. Así, el caso (c) es el de menor entropía y el caso (a) el de máxima entropía. Esto hace que la reacción (a) sea mas lenta que la (c). Mucho más lenta. Y aquí entramos en cómo la entropía gobierna la velocidad de las reacciones y la acción de las enzimas, lo cual es contenido para otro tema.

Intuitivamente, podemos expresar que en el caso (a), podemos ‘esparcir’ la energía mucho mejor que en el caso (c). Entonces, una habitación desordenada no tiene por qué ser el estado más probable, y por tanto, el de mayor entropía. Depende de cómo se distribuya la energía entre sus componentes y del número de microestados que den lugar a ese estado desordenado. Jaque mate, amigos que usais la entropía como excusa para no ordenar la habitación.

Veamos otro ejemplo intuitivo, el de una tostada con mantequilla:

Mientras la temperatura se mantenga baja y no proporcionemos calor, estaremos en un estado de baja entropía y el trozo de mantequilla se mantendrá sólido sobre la tostada. Al calentar, ¿qué es lo más probable? que la mantequilla se ‘esparza’ por la tostada. Este será un estado de mayor entropía: las moléculas de la mantequilla se separan (tiene mas ‘libertad’) y distribuyen por la tostada y la energía se reparte, ‘esparciéndose’. Aquí no hay sorpresas: tenemos un proceso irreversible (una vez esparcida la mantequilla, no podemos revertir el proceso), que se mueve, tal como nos decía Boltzmann, hacia su estado de mayor probabilidad. La mantequilla no se ‘desordena’, eso es nuestra percepción de orden y desorden, ya que antes de calentar la mantequilla no estaba formando una estructura cristalina, por ejemplo. Solo era más viscosa, dando la apariencia de ser sólida. Simplemente, la energía se ‘reparte’ siguiendo el camino más probable, aumentando los grados de libertad moleculares, o aumentando el número de microestados. Como la mantequilla es un fluido no compresible, entonces la variación de entropía sólo depende de la temperatura. Al calentarla de A a B, la entropía se incrementa según:

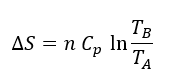
En la ecuación, n es el número de moles y Cp el calor específico. En la tostada siempre estamos cerca del equilibrio termodinámico, por lo que aquí no vamos a tener un fenómeno de estructura disipativa, que resulta de la combinación de reacciones reversibles e irreversibles interconectadas.

Estos conceptos intuitivos que relacionan la entropía no con el orden, sino con la probabilidad y con la distribución de la energía entre componentes del sistema e intercambio con el exterior, son útiles para entender la relación entre entropía, orden biólogico o para entender cómo funcionan las enzimas o la ribozima esencial que da vida a todos los organismos vivos de la Tierra: la peptidil transferasa.

Así, finalmente, la vida, como una estructura ordenada, depende de la generación de entropía y del aumento de entropía del entorno. Consumimos moléculas de alta energía para mantener nuestra estructura y, la entropía del entorno es el precio que hay que pagar por la estructura. Como dijo Schrödinger:

Cuanto más suntuoso es un palacio, mayor es el montón de basura que genera

La emisión de CO2, orina y desechos es esencial para ‘dispersar’ o ‘esparcir’ energía, aumentando la entropía del exterior. Por ello, toda organización basada en el consumo de energía siempre, por definición, es un orden temporal, cambiante y destinado a desaparecer, altamente dependiente de cual es el mecanismo por el que disipa la energía de sus fuentes de energía y del balance entre producción y disipación de entropía. Ya sea una célula, un organismo vivo o una sociedad, todas son estructuras disipativas, temporales y dependientes de la producción de entropía. Debemos estar preparados para ello.

Referencias

Cassani, A., Monteverde, A. & Piumetti, M. (2021) ‘Belousov-Zhabotinsky type reactions: the non-linear behavior of chemical systems’, Journal of Mathematical Chemistry, 59(3), pp. 792–826. doi: 10.1007/s10910-021-01223-9.

De Castro, C. & McShea, D. W. (2022) ‘Applying the Prigogine view of dissipative systems to the major transitions in evolution’, Paleobiology, 48(4), pp. 711–728. doi: 10.1017/pab.2022.7.

Harisch, K. (no date) ‘How the mind comes to life : The physics and metaphysics of dissipative structures’, pp. 1–18.

Hooker, C. (2011) ‘Introduction to Philosophy of Complex Systems: A’, in Philosophy of Complex Systems. Elsevier, pp. 3–90. doi: 10.1016/B978-0-444-52076-0.50001-8.

Howell, L., Osborne, E., Franklin, A. & Hébrard, E. (2021) ‘Pattern recognition of chemical waves: Finding the activation energy of the autocatalytic step in the Belousov-Zhabotinsky reaction’, Journal of Physical Chemistry B, 125(6), pp. 1667–1673. doi: 10.1021/acs.jpcb.0c11079.

Kondepudi, D. K., De Bari, B. & Dixon, J. A. (2020) ‘Dissipative structures, organisms and evolution’, Entropy, 22(11), pp. 1–19. doi: 10.3390/e22111305.

Naderi, M. (2020) ‘On the evidence of thermodynamic self-organization during fatigue: A review’, Entropy, 22(3), pp. 1–32. doi: 10.3390/E22030372.

Ota, K., Mitsushima, S., Matsuzawa, K. & Ishihara, A. (2014) ‘Assessing the environmental impact of hydrogen energy production’, in Advances in Hydrogen Production, Storage and Distribution. Elsevier, pp. 32–42. doi: 10.1533/9780857097736.1.32.

Shanks, N. (2001) ‘Modeling Biological Systems: The Belousov–Zhabotinsky Reaction’, Foundations of Chemistry, 3, pp. 33–53.

Tsuda, I., Yamaguti, Y. & Watanabe, H. (2016) ‘Self-organization with constraints-A mathematical model for functional differentiation’, Entropy, 18(3), pp. 1–13. doi: 10.3390/e18030074.